Rethinking NHLe

How to translate performances from one league into NHL value

Note: this article was updated on July 17th, 2023, after every players’ Win Shares from every leagues had been re-run using eTOI, changing individual Win Shares and impacting leagues as well.

The question is as old as analytics. How can we compare Connor Bedard’s 143 points in 57 WHL games with Matvei Michkov’s 20 points in 30 KHL games? What about Aydar Suniev’s 90 points in 50 games of BCHL?

If you read this, you are probably already familiar with the notion of NHLe, which tries to assign a coefficient to every league, allowing us to translate a performance from that league into NHL equivalent.

Lots of works have been done on this already, and I will simply point you toward CJ Turturo’s article as he perfectly outlined the previous researches, all the way back to Bill James’ work in baseball.

To cut it short, coefficients are drawn by using players travelling between two leagues as a proxy for assessing each league respective strength. If players scored on average 1 point per game in league A and then 0.5 point per game in league B, the coefficient between league A and B is of 0.5 as their performance is expected to diminish by half.

The first NHLe were calculated using players coming from any leagues directly to the NHL, though it limited the study to leagues in direct contact with the NHL.

Then, CJ Turturo put an existing theory into practice, creating NNHLe, or Network NHLe. Basically, creating a virtual path from any league toward the NHL, using intermediary leagues in the process, like going from the Allsvenskan, to the SHL, then the NHL.

It is fair to say most of current NHLe are now using this method and we are building on it ourselves.

Decisions and Assumptions

Like in any models, we had to make some decisions as for what data goes into it, in order to make it as less wrong as possible (stat joke here).

1/ We will be creating two NHLe, one for points and one for Win Shares.

2/ We will be mixing forwards and defensemen together, avoiding some ups and downs in data we experienced when trying to split them before.

3/ Like for our other works, we are using players moving between two leagues in adjacent seasons.

• There is a camp that believes players moving between leagues during the same season should be used only, but we disagree. Yes, players are one year older in their next league, but we observed that movement between most leagues is very age dependant (junior to second level to top senior league then back down to second level or second/third tiers leagues later in a career). So age adjustment is mostly built-in within the actual performances we will use to calculate our coefficients.

• Likewise, we also observed in previous works that movement between leagues is also extremely performance related, which sounds obvious. You have thresholds of performances that will point out if a player from the NCAA can move to the AHL or the ECHL instead.

• To wrap it up, moving from league A to league B between seasons is the consequence of those factors, and are likely to indicate a “career path” for a player, whereas a player moving between leagues during the same season introduces many more biases in our mind:

  • A moving player will have a limited sample in each league.

  • A player moves because he was too good for his first league, probably inflating his stats there. Or because his situation was too awful, for sport or personal reasons, impacting his stats as well.

  • A moving player will likely face a period of adaptation in his new league, impacting his already small sample of games.

4/ We will be using a method of Selective Network instead of using every connections existing between two leagues, like CJ Turtoro brilliantly showcased in his article. In the example below, he had calculated the NHLe between the SHL and the NHL using all those different paths.

• We chose to only be moving forwards, so when the coefficient between two leagues is inferior to 1, indicating that we are progressing from an inferior league to a better league.

• A player needs to have played at least 10 games in both leagues to to be considered. And we are limiting ourselves to paths used by at least 20 players in the past 15 years. We also removed the NHLers that played abroad during the last lockouts.

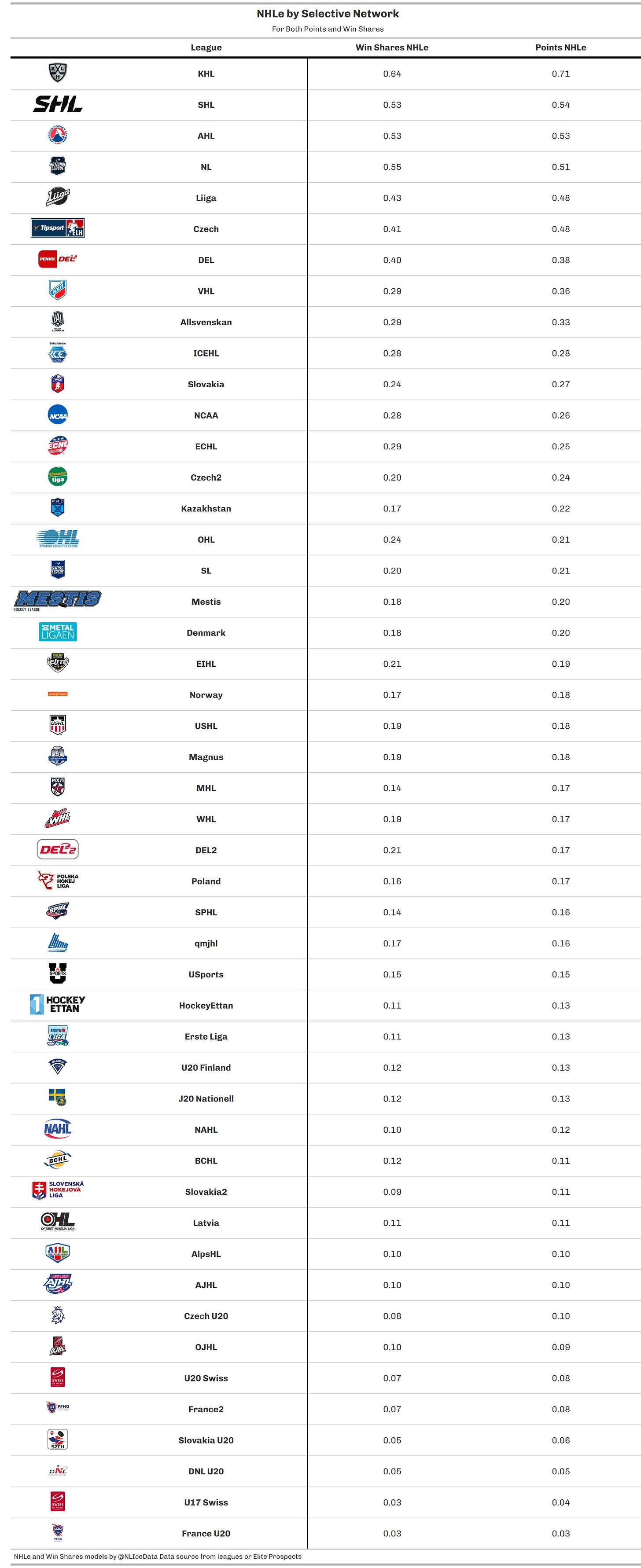
Selective Network NHLe

Selective means establishing a pyramid system building up the path to the NHL, which implies making subjective choices at some point so the path makes the most sense.

• First selective choice was to name both the AHL and the KHL as independent final steps before the NHL. Technically, the AHL could have used another path going through the KHL but we felt it irrelevant here as AHLers going to Russia are mostly older players when AHLers moving to the NHL are prospects or in their prime career.

  

• We have some 2,098 AHLers who played at least 10 games in the NHL the next season, with a coefficient of 0.53 for points and 0.53 as well for Win Shares, meaning they scored 0.53 point in the NHL for 1 point in the NHL. We also have 113 KHLers who played in the NHL the next season, with a 0.71 coefficient for points and a lower 0.64 coefficient for Win Shares, showing these KHLers are more scorers than overall contributors at the NHL level.

• Second choice was to sometimes remove some paths, like when both the Swiss NL and the SHL have a mutual positive coefficient between each other, making the path more blurry than necessary (note: it only happened in one other instance, when all of EIHL, Denmark, Norway and DEL2 were feeding each others in a circle).

So, for example, both the NL and the SHL have three paths in their networks, going either directly to the NHL, or through the AHL or KHL. We then weighted each path according to how many players went through it and calculated the final NHLe.

For the SHL, 51% of players progressing to a better league went to the AHL, 32% went to the KHL and 17% went directly in the NHL. The calculation for each path is simply to multiply its components with each others:

                   SHL > KHL > NHL for points = 0.75 * 0.71 = 0.53
                   SHL > AHL > NHL for points = 0.99 * 0.53 = 0.52
                   SHL > NHL for points = 0.64 (you can see we have better players here)

Using the weighted elements NHLe = (0.53 * 32%) + (0.52 * 51%) + (0.61 * 17%) 

Which gives us NHLe = 0.543 (using more decimals everywhere) for points for the SHL, while the NHLe for Win Shares would be 0.525.

Down the ladder

Then we repeated the process for all the other leagues, as soon as their needed paths to the NHL had been established. Next in line was the Finnish Liiga, as we needed to establish the final NHLe for SHL and NL as both leagues are paths from Liiga to the NHL. Same for the German DEL.

After Liiga and DEL were calculated, the Czech Extraliga was up, with paths going through: AHL, DEL, KHL, Liiga, NL, SHL and directly to the NHL. But the Swiss second level, which only goes through the NL and DEL was calculated as well, same for the Russian VHL that only needed a KHL bridge.

As we went down the ladder, the networks do not necessarily get more complicated, we just needed to connect more leagues together. The longest network was for Swedish U20, having 9 different paths in it, going through (by weight) HockeyEttan, Allsvenskan, SHL, USHL, Norway, OHL, Denmark, WHL and NCAA. But for many of the smaller leagues, only a handful of paths were necessary, like Poland only connecting to Slovakia, Czech2 and Slovakia2 (then their subsequent networks).

And we arrived at the following ranking.

How relevant are NHLe?

Last but not least, how good are these NHLe compared to actual direct links between two leagues? Meaning, if we compare the NHLe of two leagues, say Poland (NHLe 0.157) and Denmark (NHLe 0.182), I can derive a coefficient for players going from Poland to Denmark of 0.157 / 0.182 = 0.86. If I want to compare these coefficients derived from NHLe values with actual coefficients existing between two leagues, using leagues with at least 10 links between them, I get a r2 = 0.91. Pretty sweet.

And it goes up to 0.93 if I compare to leagues with 20 links. Safe to assume that comparing NHLe is a good proxy for comparing leagues.

So now we have a tool for further analysis…